Here’s some math empowerment

Note: In 2021, I’m writing one blog post per week. It’s a little confusing, but this entry is both a placeholder of sorts for Week 18 (approx May 3 to May 8) — just the second time this year so far that I’ve missed my self-imposed weekly deadline — and a new post for Week 19 (approx May 9 to May 15).

Note (added 22 May 2021): Here are some extra links readers might find useful on this topic. A list of online resources for learning math free of charge, the helpful r/math subreddit FAQ, and mathematician Paul Lockhart’s well-known 25-page essay, sometimes called Lockhart’s Lament, decrying how math is typically taught in schools and providing suggestions for how to teach the subject as discovery and art. He later developed his essay into a book (which I haven’t read), titled A Mathematician’s Lament.

Teaching stress led me to skip another week. But! I’m back now. My 67-workday assignment — substitute-teaching high school geometry — ends on May 20, so that should free me up to dedicate more time to my blog: the globe’s most well-regarded and high-profile publishing outlet, far surpassing the London Review of Books, Asimov’s, and the nonexistent Fancypants Publishing, all combined. Starting next week, I’ll try to begin each post with a few bullet-point news blasts (before the post proper gets underway), since many of my readers aren’t on twitter where world events, unamplified or underamplified in the United States, enter international public awareness for the first and sometimes only time.

To make quick work of this blog entry, I’ll share with you four math videos off youtube that I, and hopefully the students, found helpful. The first three are about trigonometry; the last is a “map of mathematics” which shows how the subject covers much more than usually addressed in boredom torture chambers school. The initial video is three minutes and by the BBC. It credits the ancient Greeks with discovering trigonometry before anyone else; I don’t know if that’s really true… I have my doubts. What I like is how the BBC video superimposes a triangle on a building structure, and then later shows how a triangle can similarly be superimposed to find out (in relative terms) how much farther the Sun is from us than the Moon is from us. Teachers can project such a video onto the markerboard at the front of the classroom, pause it before the video gives the answer, and have students work out the problem themselves at their desks. Compared with teachers hand-drawing stick figures with a dying dry-erase marker, a high-resolution graphic on the board is way more fascinating as a word problem (judging by student reactions). The other two trigonometry videos, by Numberphile and Tibees, helpfully show the connection between trigonometry and circles. We too often think of trigonometry as about triangles (trigon comes from Greek’s τρίγωνον for triangle). Trigonometry is about triangles, but it’s also about circles. I hope you enjoy the videos… Next to memorizing math mechanics for endless drills of practice problems, patiently understanding why and how math really works is much more fun and opens up great appreciation for the mind and for Nature.

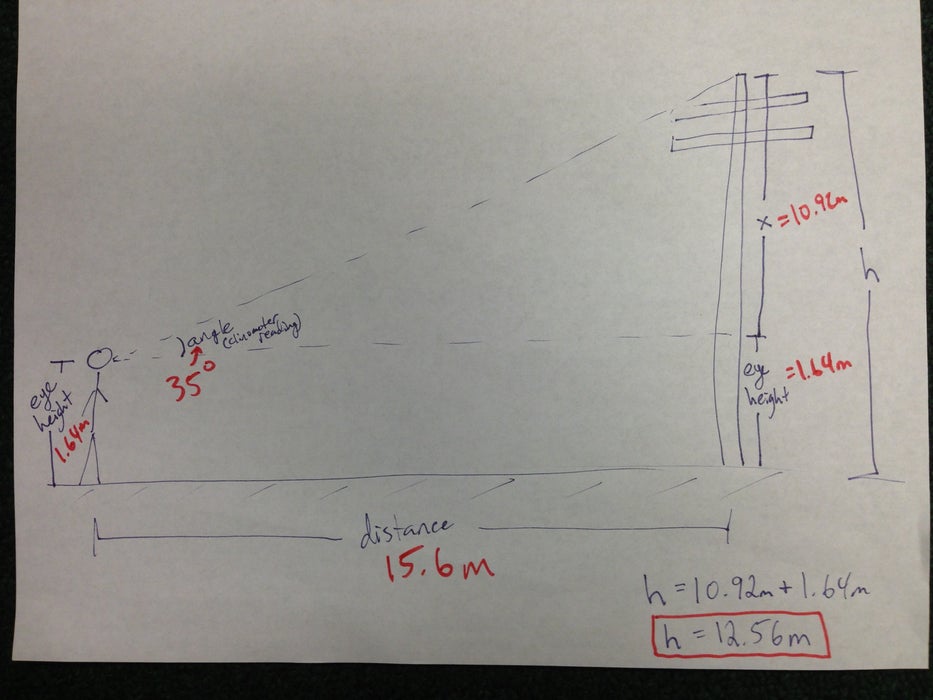
Oh! There’s also a neat in-person trigonometry exercise teachers can do with students, or autodidacts can do teaching themselves. Basically, you make a DIY clinometer out of common materials — fishing line worked well for me as the string — to sight the degrees of an angle, and then with a tape measure and trigonometry (the tangent function), you calculate the height of an object such as a lamppost. This can be helpful in engineering as it might be impractical to physically measure a tall object. In two of my periods, we found the height of the basketball goal on campus grounds, from pavement to hoop. The first class hit the answer perfectly: about 3 meters (about 10 feet, regulation height). The second class arrived at about 3.2 meters (about 10.5 feet), probably because the tape-measuring of the adjacent triangle side (the distance of pavement between right-below-the-hoop and where the student sighted the angle) was a bit inexact. All in all, the trigonometry exercise was a vivid way to explore math in the empirical world.

Exercises like trigonometry with a DIY clinometer startle me into remembering how in our reliance on addictive technology or on what other people pretend to know (especially celebrities or those with power over us), we tend to forget, or never learn in the first place, why and how things like GPS on smartphones actually work: i.e., how does a phone actually know where on the planet it’s located? (GPS involves trigonometry.) Besides math, what critical minerals is a smartphone made out of anyway, minerals the mining of which destroyed lives and communities? Even something as DIY-simple as putting together a clinometer and doing some straightforward math outdoors feels like — and actually is — a method of resisting corporate/military dominance (along with the constant anxiety and danger under it) by strengthening yourself, taking back power. Because, instead of depending on (often unknowledgeable) others or merely taking things for granted, with math (and other education) you gain a better understanding, scary as it sometimes can be, of how the world and life truly work.

This blog post, Here’s some math empowerment, by Douglas Lucas, is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License (human-readable summary of license). The license is based on a work at this URL: https://douglaslucas.com/blog/2021/05/15/shucks-missed-entry18-math-empowerment/ You can view the full license (the legal code aka the legalese) here. For learning more about Creative Commons, I suggest this article and the Creative Commons Frequently Asked Questions. Seeking permissions beyond the scope of this license, or want to correspond with me about this post one on one? Email me: dal@riseup.net.

Note: In 2021, I’m writing one blog post per week. It’s a little confusing, but this entry is both a placeholder of sorts for Week 18 (approx May 3 to...